|
Lost Tech Archive |
By Ivars Vilums - August, 1990 (originally published in my "Underware Labs" web site in 1997)
This paper attempts to show that a sufficiently short electromagnetic wave will undergo gravitational collapse. It will derive a value for the size of this wavelength, and speculate on some of the ramifications of this phenomenon.
It is well known that, for an electromagnetic wave, as the wavelength decreases the energy of the wave increases. It is also well known that energy and mass are equivalent. It has been demonstrated many times that electromagnetic waves are affected by gravitational fields and that electromagnetic waves exhibit the mass equivalent of the energy of their wavelength. It is also accepted that when a mass is concentrated in a sufficiently small enough space, it will undergo gravitational collapse. The radius of this space for any mass is called the Schwarzschild radius.
Starting with an expression for determining the Schwarzschild radius as a function of mass value and an expression of energy as a function of wavelength, we will derive an expression to determine the mass equivalent of any wavelength of electromagnetic energy. Knowing this, we can then derive a relationship that expresses the Schwarzschild radius of any wavelength. Since energy increases as wavelength decreases, we can then solve for the wavelength size that will have a sufficient energy density in a space whose size is equal to the Schwarzschild radius for its equivalent mass.
Expressing the Schwarzschild Radius as a function of Mass:
The relationship
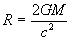[Equation
1]
shows how the Schwarzschild radius for any mass M is related to the gravitational constant G and the speed of light c.
G and c have been measured as
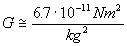[Equation
2]
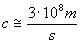[Equation
3].
Substituting the expressions of [2] and [3] for G and c and using kg as the unit of mass we can thus express [1] as
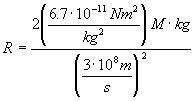[Equation
4]
which reduces to
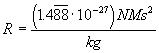[Equation
5].
By definition
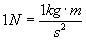[Equation
6].
Thus, by substituting the expression in [6] for N, [5] can be expressed as
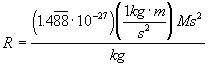[Equation
7]
which, through cancellation, reduces to
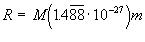[Equation
8].
Deriving Energy as a function of wavelength:
It has been shown that the energy of an electromagnetic wave is related to its frequency by the relationship
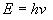[Equation
9]
and the frequency of an electromagnetic wave is related to its wavelength by the relationship
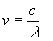[Equation
10].
Plank's constant, h, has been measured at
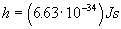[Equation
11].
Substituting the expressions in [3], [10] and [11] for c, h, v and using units, we can express [9] above as
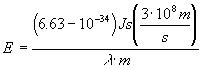[Equation
12].
By canceling m and s and simplifying we derive the relationship
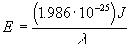[Equation
13].
Deriving Mass as a function of wavelength:
Given that energy as a function of mass is expressed by the relationship
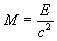[Equation
14],
if we substitute the expression in [13] above for E and the expression in [3] above for c, we can restate [14] as
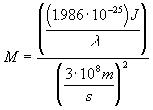[Equation
15]
which can be simplified to
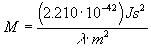[Equation
16].
Since, by definition,
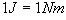[Equation
17]
and
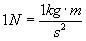[Equation
18],
by substituting the expression in [18] for N in [17] above, we can state that
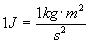[Equation
19]
and substituting this expression for J in [16] above, we obtain
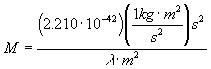[Equation
20]
which, by canceling m2 and s2 reduces to
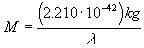[Equation
21].
Deriving the Schwarzschild Radius as a function of electromagnetic wavelength:
Substituting the expression of [21] above for M in [8] above, while taking into account the cancellation of the kg factor of [21] between steps [7] and [8] above, yields the relationship
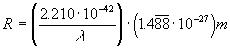[Equation
22]
which can be simplified to
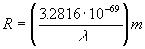[Equation
23].
Deriving the Schwarzschild wavelength:
We can now calculate using [23] the Schwarzschild radius for any wavelength of electromagnetic radiation. Since, as the wavelength gets shorter, the energy in the wave (and thereby also its equivalent mass) increases, it is apparent, then, that there is a wavelength sufficiently short enough that it is shorter than the Schwarzschild radius of the energy in the wave.
The wavelength equal to this size can be computed by modifying [23] above to take into account the two energy peaks in a wave. The relationship is
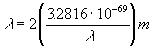[Equation
24].
Finally, solving for we find that
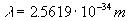[Equation
25] .
Thus, electromagnetic waves with wavelengths shorter than 2.5619 * 10-34 meters will undergo gravitational collapse.
Symbols used:
Note: units of measurement are used explicitly.
Questions and further inquiry:
copyright 1990 by Ivars Vilums. All rights reserved.
